We first observe a relationship between the number of cuts and the number of points of intersection, and the number of slices obtained. Suppose we have made $n$ cuts, and these $n$ cuts intersect in $k$ points on the cake, and furthermore assume that no three cuts go through the same point. We claim that the number of slices is $F(n,k):=n+k+1$ .

We can prove this formula by induction. The first cut slices the cake into two parts, so $F(1,0)=2$ as the formula dictates. Now given $F(n,k)$, suppose we create a new cut which intersects the previously made cuts in $m$ distinct points.

Then we cut into exactly $m+1$ previously made slices, and cut all of these into two. This gives

$$F(n+1, k+m)=F(n,k)+m+1=n+k+1+m+1=(n+1)+(k+m)+1.$$

Observe furthermore that we must have $m \leq n$, because a new cut can only intersect each previous cut at most once, and so – again by a formal induction – we find that if $n$ cuts have $k$ points of intersection, then $k \leq 1+\ldots +n=\frac{n(n+1)}{2}$.

It is easy to see that the number of slices on $n$ cuts is at least $n+1$, which is achieved with $k=0$ intersection points. For an upper bound, notice that if we have multiple cuts going through the same point, then we can always increase the number of slices by adjusting the cuts slightly so that the intersection points become pairwise distinct. Therefore an upper bound is given by

$$F(n,n(n+1)/2)=n+\frac{n(n+1)}{2}+1=\frac{(n+1)(n+2)}{2}.$$

We claim that any number between these two values is possible to obtain (including the bounds themselves), or in other words, for every $0 \leq k \leq \frac{n(n+1)}{2}$, there is a configuration of $n$ cuts on the cake with exactly $k$ intersections. More abstractly, we want to show that there is a configuration of $n$ straight lines and a circle such that the circle intersects all $n$ lines and contains exactly $k$ of their intersection points.

First, observe that $k=\frac{n(n+1)}{2}$ is achievable by taking $n$ straight lines which all intersect in distinct points, and taking a large enough circle containing all intersections. We will show that we can always decrease the intersection points by $1$, that is, if there is a configuration of $n$ lines and a circle with $k \geq 1$ pairwise distinct intersection points inside the circle, there is also one with $k-1$.

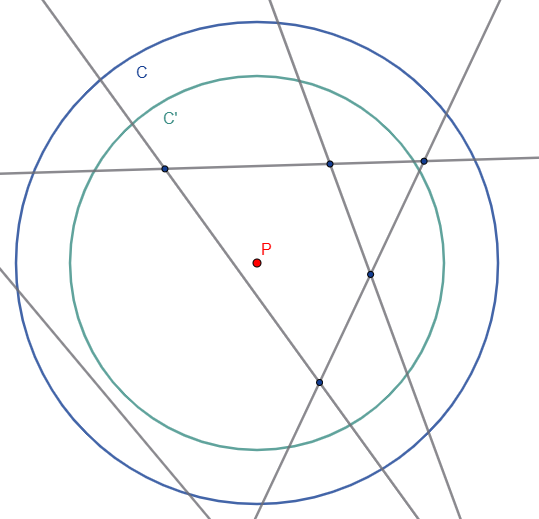
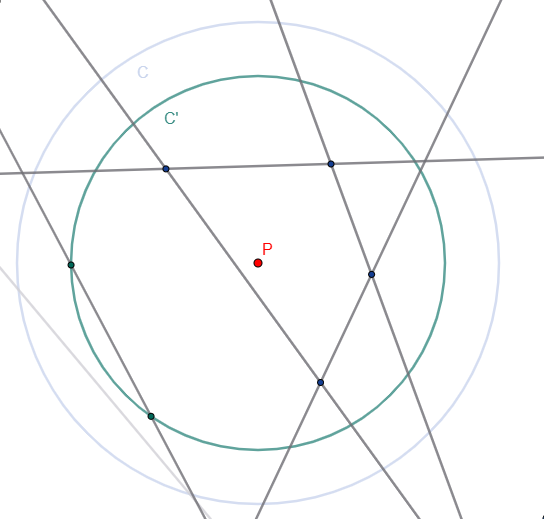
Take a configuration of straight lines and a circle $C$ such that $C$ intersects all lines, contains exactly $k$ intersection points, and there are exactly two lines meeting at each intersection point. Assume furthermore that no two intersections are exactly the same distance from the centre $P$ of the circle – this can always be achieved by moving the circle slightly. Start shrinking $C$ from its centre $P$ until it no longer contains the intersection point with maximum distance from $P$, and denote the shrunken circle by $C'$ (see first picture below). This clearly contains $k-1$ intersection points by construction. If $C'$ still intersects all $n$ lines, then this is a good configuration. Otherwise, for every line that $C'$ no longer intersects, we add a new line which intersects $C'$ but does not intersect any other lines within $C'$ – this can always be done by choosing two points on an uninterrupted arch of $C'$ and connecting these (see second picture below).

It follows (again by a formal induction) that a configuration is possible for any $k$ between the identified bounds. Fixing $n=2025$, $k$ (and thus $F(2025,k)$) can take $\frac{2025(2026+1)}{2}+1$ different values.

Answer: 2049301.

Let us try to find another square-loving year among the $4$-digit ones. Denote by $x$ and $y$ the integers formed by the first two and last two digits. For a square-loving year we have that:

$$100x + y = (x+y)^2.$$

By rearranging terms we get:

$$99 x = (x+y)(x+y-1).$$

In particular, $(x+y)(x+y-1)$ is a multiple of $99$. Note that $x+y$ and $x+y-1$ are co-prime, allowing us to conclude that one of them is a multiple of $9$ and one is a multiple of $11$.

• Case 1. $x+y$ is a multiple of both $9$ and $11$, i.e. a multiple of $99$. Since $x, y \leq 99$ and $x+y > 0$, we have that either $x+y = 99$ or $x+y = 198$.
  • Case 1.1. $x+y = 99$. In that case $x+y -1 = x$, leading to $y=1$ and $x=98$. The year $9801$ is indeed square-loving.
  • Case 1.2. $x+y = 198$. This means $x = y =99,$ but $9999$ is not a square-loving year, meaning that our assumption is incorrect.
• Case 2. $x+y$ is a multiple of $9$ and $x+y-1$ is a multiple of $11$. Denote $\frac{x+y}{9}$ by $z$, and note that $z<\frac{198}{9} = 22$. We have $11x = z (9z -1)$. Since $z$ is not divisible by $11$, $9z -1$ must be divisible by $11$. Write $z = 11k + r$, $k\geq 0$, $0 \leq r \leq 10$. We get $99k + 9r - 1$ is divisible by $11$, meaning that $9r -1$ is divisible by $11$. It is straightforward to see that only $r=5$ satisfies these constraints. Thus, $z = 5$ or $z = 16$. Consequently, $11 x = 220$ or $11 x = 2288$. Only the first option satisfies $x < 99$, implying $x = 20$ and $y=25$. The year $2025$ is also square-loving.
• Case 3. $x+y$ is a multiple of $9$ and $x+y-1$ is a multiple of $11$. Denote $\frac{x+y}{11}$ by $z$ and note that $z<\frac{198}{11} = 18$. We have $9 x = z (11 z -1)$. Since $z$ is not divisible by $3$ or by $9$, $11z -1$ must be divisible by $9$. Write $z = 9k + r$, $k\geq 0$, $0 \leq r \leq 8$. We get $99k + 11r - 1$ is divisible by $9$, meaning that $11r -1$ is divisible by $9$. It is straightforward to see that only $r=5$ satisfies these constraints. Thus, $z = 5$ or $z = 14$. Consequently, $9 x = 270$ or $9 x = 2142$. Only the first option satisfies $x < 99$, meaning that $x = 30$ and $y=25$. The year $3025$ is also square-loving.
• Case 4. $x+y-1$ is a multiple of both $9$ and $11$, i.e. a multiple of $99$. Since $x, y \leq 99$ and $x+y > 0$, we have $x+y -1 = 99$. However, this means $x+ y = x$, giving us $x = 100$ and $y =0$, which contradicts the established constraints. Thus, our assumption is incorrect.

Following this comprehensive analysis, we can conclude that $9801$ is the next (and only remaining) square-loving year.

Answer: 9801.

Consider the way one can pay $15$ pounds in Totalia using at most $14$ coins. Since $x^k$ is irrational by assumption, we cannot get away with using only 1-pound coins together with a singular type of $x^k$-pound coins as these will only give irrational amounts above $14$. Furthermore, $x^3 > 27$, so we can use only the coins of the value $1$, $x$ and $x^2$ to pay $15$ pounds.

However, $x^2 +x + 1 > (3.3)^2 + 3.3 + 1 = 15.19$, meaning that we cannot use $1$ either, and we can also not use more than one of each $x$ and $x^2$ coin. Thus the only possibility is if $x^2 +x =15$, which has a positive solution:

$$x = \frac{\sqrt{61} - 1}{2} \approx 3.4051.$$

This is indeed irrational and bigger than $3.3$ and hence satisfies our assumption.

Note that this $x$ also allows us to pay any positive integer sum by iteratively exchanging $15 x^k$ for $x^{k+1}$ and $x^{k+2}$ until no denomination is used more than 14 times.

Answer: 3.4051.

Consider a sequence of moves that starts in $256$ Hz. Assume that we have done $a_1$ moves of type 1, $a_2$ moves of type $2$, $a_3$ moves of type 3' and $a_4$ moves of type of 4'. Note that if we use both moves of type 1 and type 2, they cancel out. A similar statement holds for types 3' and 4'. Thus, if we are concerned with distinct results, we only need to consider $b = a_1 - a_2$ and $c = a_3 - a_4$. The resulting frequency is $256 \cdot 2^b \cdot (\frac{3y}{2})^c$. Thus the frequencies we can obtain in an octave by using the approximation $y$ is exactly the number of different solutions for the inequality

$$256 \leq 256 \cdot 2^b \cdot (\frac{3y}{2})^c < 512$$

for integers $b,c$.

Let $y_0$ denote the approximation referenced in the problem, that is $y_0 \approx 0.99887$. The question is then the following. Assume $y \in \mathbb{R}^+$ is a fixed approximation such that the number of solutions for the inequality above is finite, and furthermore suppose that $y$ is a better approximation of $1$ than $y_0$, that is, $|y-1| < |y_0- 1|$. What is the smallest possible number of solutions?

We can simplify it further by taking the logarithm with base 2 from all the parts of the expression, obtaining

$$8 \leq 8 + (b-c) + c \cdot \log_2(3y) < 9.$$

To simplify it even further, denote $d = b-c$ and $z = \log_2(3y)$ (note that $z>0$ by our constraints) as both pairs of variables can be uniquely determined by the other. Finally, we have

$$0 \leq d + c z < 1.$$

Note that if the number of solutions is finite, $z$ must be a rational number. In order to see that, consider the smallest number $x$ which is a solution and suppose $x = d_x + c_x z$. If $x$ is irrational, there exists an integer $n$ such that $\frac{1}{n+1} < x < \frac{1}{n}$. It follows that $0<(n+1)x-1 < x$. However, $(n+1)x-1$ is also a solution (with $d=(n+1) d_x -1 , c=(n+1) c_x $), which contradicts our choice. Thus, $x$ is rational and $z = \frac{x-d_x}{c_x}$ is also rational.

If $z = \frac{p}{q}$ where $p,q$ are coprime positive integers, the number of solutions is equal to $q$ as we can achieve any fraction $\frac{r}{q}$ for $0 \leq r < q$. In order to see this, it is suffices to demonstrate that there exist integers $d,c$ such that $d + c \frac{p}{q} = \frac{1}{q}$, or equivalently $dq + cp =1$, in which case we have $dr + cr \frac{p}{q} = \frac{r}{q}$. Such $d$ and $c$ indeed exist by Bézout's identity.

The key is thus to find the smallest possible $q$ such that $z=\frac{p}{q}=\log_2(3y)$ is a closer approximation of $\log_2 3$ than $\log_2(3y_0)$. We also see from the argument above that $\log_2(3y_0)$ is a rational number with denominator $12$ (it is in fact $19/12$), hence giving the $12$ notes in an octave.

It is possible to find $q$ just by methodically checking all fractions, starting from low denominators, until we first find a better approximation for $\log_2 3 \approx 1.585496$ then $\log_2(3y_0)=19/12 \approx 1.583334$. However, there is a much more efficient way to do this using Farey sequences.

The Farey sequence of order $n$ is the collection of all completely reduced fractions with denominators of $n$ or less, arranged in increasing order. It is known that if $\frac{p_1}{q_1}, \frac{p_2}{q_2}$ are neighbours in the sequence of order $\max(q_1,q_2)$, then the first fraction to appear between them in some higher order Farey sequence is $\frac{p_1 + p_2}{q_1+q_2}$. This gives us the following method to find rational approximations with minimal denominators.

Consider a number $x$ to approximate by rational numbers. Assume that we already have upper and lower approximations $\frac{p_1}{q_1} < x < \frac{p_2}{q_2}$, where $\frac{p_1}{q_1}, \frac{p_2}{q_2}$ are neighbours in the Farey sequence of order $\max(q_1,q_2)$, meaning that they are the best upper and lower approximations with denominator at most $\max(q_1,q_2)$. Then the next best approximation will be $\frac{p_1 + p_2}{q_1+q_2}$, giving us either $\frac{p_1}{q_1} < x < \frac{p_1 + p_2}{q_1+q_2}$ or $\frac{p_1 + p_2}{q_1+q_2} < x < \frac{p_2}{q_2}$. Iterating this process, we can continue to find closer upper and lower approximations, while always minimizing the denominator required for each approximation. At any step, whichever of the upper/lower approximations is closer to $x$ will be the best rational approximation with the same denominator or lower.

Let us apply this method to $x= \log_2(3) \approx 1.58496$. The Farey sequence of order $1$ gives us $\frac{1}{1} <x <\frac{2}{1}.$ By the process described above, we further obtain

• $\frac{3}{2} =\frac{1+2}{1+1} <x <\frac{2}{1}.$
• $\frac{3}{2} <x <\frac{3+2}{1+2} = \frac{5}{3}.$
• $\frac{3}{2} < x < \frac{3+5}{2+3} = \frac{8}{5}$
• $\frac{11}{7} = \frac{3+8}{2+5} <x <\frac{8}{5}.$
• $\frac{19}{12} = \frac{11+8}{7+5} <x <\frac{8}{5}.$
• $\frac{19}{12} <x < \frac{19+8}{12+5} = \frac{27}{17}.$

However, $\frac{19}{12}$ is closer to $x$ than $\frac{27}{17}$. Thus, we require another step giving us $\frac{19+27}{12+17} = \frac{36}{29}$, which is indeed closer to $x$ than $\frac{19}{12}$. Thus, we have $q=29$.

Remark: it is in practice more efficient to first find rational approximations of the fractional part of $x$, and then obtain the rational approximations of $x$ by simply adding the floor of $x$. This makes the enumerators in the calculation smaller and hence slightly easier to work with.

Answer: 29.

Let $w_1$ be a child that gets wet, and let $w_2$ be the child who was hit by $w_1$s balloon. Suppose the distance between them is $r$. We are going to find an upper bound on the number of children who threw their balloons at either $w_1$ or $w_2$.

First, observe that there is nobody within an $r$ radius of $w_1$. Next, observe that if we draw the perpendicular bisector between $w_1$ and $w_2$ as in the picture below, any child on the left of the perpendicular bisector who targets $w_1$ or $w_2$ must target $w_1$, and any child on the right of the perpendicular bisector who targets $w_1$ or $w_2$ must target $w_2$, while anyone on the perpendicular bisector may freely choose between $w_1$ and $w_2$.

Lastly, observe that if children $a$ and $b$ each throw at some child $w$, then the angle $V$ of triangle $awb$ at $w$ must be at least $60^\circ$, otherwise $a$ and $b$ would be too close to each other to choose to throw at $w$.

Now section the plane into $60^\circ$ wedges extending out from $w_1$ and $w_2$ as shown below. We let the perpendicular bisector be an additional border, and we let each section include its clockwise border, as indicated by the colours. We may assume that anyone standing on the upper part of the perpendicular bisector who targets $w_1$ or $w_2$ chooses $w_1$ and anyone standing on the lower part of the perpendicular bisector who targets $w_1$ or $w_2$ chooses $w_2$. Number the sections 1 through 8, as shown below:

It follows that there can be at most one child targeting $w_1$ in each of sections 1 through 4, and at most one child targeting $w_2$ in each of sections $5$ through $8$. This gives us an upper bound on the number of children who could be in the game: if there are $k$ children that get wet, there are at most $5k$ players in the game. Now, when $k$ is even, we can actually attain this upper bound in the following way. Put the wet students in pairs. For a pair of wet children, say $w_1$ and $w_2$, have $w_1$ and $w_2$ throw at each other. Then, surround $w_1$ and $w_2$ with dry students who target $w_1$ and $w_2$ in the following way:

If the pairs of wet children are spread sufficiently far from each other, we can surround each pair in this way, attaining the maximum number of children playing at 10 total children per pair. This means that for 12 wet children, we can form 6 pairs and attain a total of 60 children playing the game.

Answer: 60.

Before we begin to answer the question, it is useful to make some general observations about the behaviour of the light feature.

First observe that if we at any time press all buttons on the grid, we invert the pattern (that is, turn off all the lightbulbs that were on and vice versa). This is because each lightbulb will experience exactly 89 switches (there are 89 buttons which share a row or a column with a given lightbulb), and odd number of switches causes it to change its state.

Thus, the number in question can be found by answering a different question: starting with all bulbs on and pressing some buttons, what is the smallest possible number of lightbulbs which can be on at a given time, if at least one lightbulb is on? Furthermore, since we can switch the initial position from "all on" to "all off" and from "all off" to "all on" by pressing all the buttons, it is equivalent to the following: starting with all bulbs off and pressing some buttons, what is the smallest possible number of lightbulbs which can be on at a given time, if at least one lightbulb is on?

Consider a position of the grid reached by pressing some switches starting with all lights off. We claim that if we press all the buttons in positions where the lights are on (let us call this Big Shutdown), we will turn the whole grid off.

To see this, consider any given lightbulb. We will prove that if it is off, then the union of its row and column contains an even number of lights that are on (thus, preserving its state under the Big Shutdown), and if it is on, then the union of its row and column contains an odd number of lights that are on (thus, switching its state under the Big Shutdown).

Initially, when all the lights are off, the two properties above are evidently satisfied (zero is even). Now, for a proof by induction, assume that these properties are satisfied for some configuration of on-off lightbulbs. We want to demonstrate that they are still satisfied after a single press of a button. Assume the button we pressed has coordinates $(x_0,y_0)$, where $x_0$ is the row and $y_0$ is the column, and consider an arbitrary lightbulb with coordinates $(x,y)$.

• Case 1. $x = x_0, y = y_0$. The state of the lightbulb changed, and the parity of "on" lights in the union of its row and column also changed: there are 89 lightbulbs, all of which changed states. Thus, the properties are preserved.
• Case 2. $x=x_0 , y \neq y_0$. The state of the lightbulb changed, and the parity of "on" lights in the union of its row and column also changed: there are 89 lightbulbs, 44 of which, corresponding to the column, did not change states, and 45 of which, corresponding to the row, changed states. Thus, the desired properties are preserved.
• Case 3. $x \neq x_0 , y = y_0$. This is similar to Case 2.
• Case 4. $x \neq x_0 , y \neq y_0$. The state of the lightbulb changed, and the parity of "on" lights in the union of its row and column also did not change: there are 89 lightbulbs, 2 of which, corresponding to $(x,y_0)$ and $(x_0,y)$, changed states, and 87 of which did not change states. Thus, the desired properties are preserved.

Consequently, if any button press preserves the properties and they are satisfied initially, they must always hold, and so the Big Shutdown does indeed turn the grid off.

We now arrive to a key observation: we claim that if there is at least one lightbulb on, then there is at least one lightbulb on in every row and column, otherwise the Big Shutdown would not work. This clearly gives a lower bound of $45$ for the least amount of lightbulbs that can be on in any achievable configuration.

We show the claim by contradiction. Assume that there exists a configuration which is turned down by the Big Shutdown with at least one bulb on and with a row $n$ entirely off (the case for columns is similar). Since the Big Shutdown works, we have that every column must have an even number of lightbulbs which are on. However, consider any lightbulb which is on: its row (different from $n$ by our choice) must have an even number of lightbulbs which are on (to give us an odd number of bulbs which are on in the union of its row and column - sum of even numbers minus one for the original lightbulb being counted twice). This means that there is a lightbulb which is off in the same row (as 45 is odd, not even). However, the Big Shutdown will cause this new "off" lightbulb to switch its state by the same argument, resulting in a configuration where not all bulbs are off. This is a contradiction.

Hence, at least 45 lightbulbs must be on.

The number 45 is achievable by pressing all the buttons corresponding to the bulbs on one of the diagonals of the grid: it is straightforward to see that these bulbs will turn on, while all the others will remain off.

In order to obtain the final answer, we must remember to use the inversion described in the beginning of the proof, giving us $2025- 45 = 1980$ lightbulbs.

Answer: 1980.

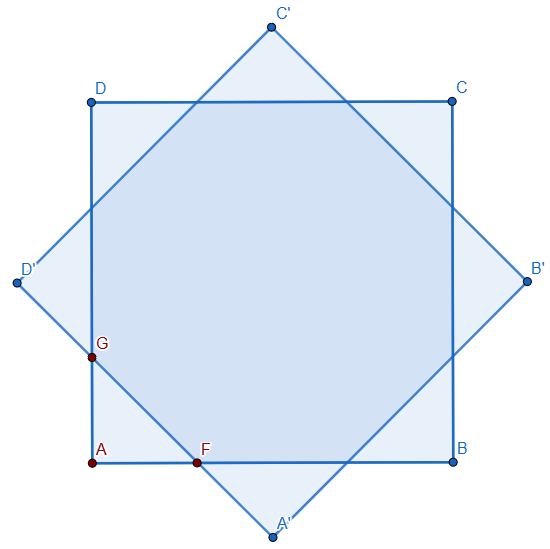
Let $ABCD$ represent the bottom chessboard, and $A'B'C'D'$ the top chessboard, which is the image of the square $ABCD$ under a $45^\circ$ rotation about the center.

We begin by showing that the overlap of black squares is exactly a quarter of the overlap between the two boards. Denote the latter area by $T$. Let $T_{bb}$, $T_{wb}$, $T_{bw}$, $T_{ww}$ respectively denote the areas where the top and bottom board are both black; where the top is white and the bottom is black; where the bottom is black and the top is white; and where both the top and bottom are white. It is clear that $T=T_{bb}+T_{wb}+T_{bw}+T_{ww}$.

Observe that mirroring both chessboards about the axis $AC$ leaves the pattern of $ABCD$ unchanged, but swaps the white and black squares in $A'B'C'D$. It follows that $T_{bb}=T_{bw}$ and $T_{wb}=T_{ww}$. Similarly, mirroring onto the line $A'C'$ leaves the pattern of $A'B'C'D'$ unchanged, but swaps the colors in $ABCD$, which yields $T_{bb}=T_{wb}$ and $T_{bw}=T_{ww}$. It follows that $T=4T_{bb}$ as claimed.

We now calculate $T$. Note that the area of $ABCD$ is $64$, so it suffices to calculate the area of the triangle $AGF$, as $T=64-4T_{AGF}$. Observe that $AG=GD'=AF=FA'$, denote this length by $a$. Denoting the length $FG$ by $c$, we first observe that $A'D'=A'F+FG+GD'=2a+c$, and by the Pythagorean theorem for $AGF$, we have $2a^2=c^2$. This yields the quadratic equation:

$$2a^2=(8-2a)^2,$$

which has one solution between $0$ and $8$, namely $a=8-4\sqrt 2$. We have $T_{AGF}=a^2/2$. Then:

$$T_{bb}=\frac{64-2a^2}{4}=32(\sqrt 2-1)\approx13.2548.$$

Answer: 13.2548.

Note that for any integer $n$, light number $m$ flashes on the $n$th second if and only if $m$ divides $n$. This means that if the first time exactly $2025$ lights flash up is after $n$ seconds, then $n$ is the smallest number that has exactly $2025$ distinct factors below $2^{2025}$.

Given $n$, consider its decomposition into prime factors: $$n= p_1^{\alpha_1} \cdots p_k^{\alpha_k},$$ where $k \ge 1, \alpha_i \ge 1$ and $p_i$'s are distinct prime numbers. It is straightforward to see that $n$ has exactly $(\alpha_1+1) \cdots (\alpha_k +1)$ distinct factors in total, as each factor $m$ must have the form $$m= p_1^{\beta_1} \cdots p_k^{\beta_k},$$ where $0 \le \beta_i \le \alpha_i$.

Let us start with finding the smallest number $n_0$ which simply has exactly $2025$ distinct factors. If $n_0 < 2^{2025}$, it already satisfies the desired criteria.

Let $n$ be any number with 2025 distinct factors. Considering the prime factorisation above we get $$(\alpha_1+1) \cdots (\alpha_k +1) = 2025 = 3^4 \cdot 5^2.$$

Note that if the collection of values for $\alpha_1, \ldots, \alpha_k$ is fixed, we obtain the minimal corresponding $n$ by assigning the smallest possible prime (namely, $2$) to the largest power, the next prime (namely, $3$), to the second-to-largest power, and so on. Thus, we need to compare different possible factorisations of $2025$ and the corresponding $n$'s while assuming $\alpha_1 \ge \cdots \ge \alpha_k \ge 1$ and $p_1 = 2, p_2 =3, \ldots$.

Consider the maximal possible $k$, corresponding to $$5\cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = (4+1) (4+1) (2+1)(2+1)(2+1)(2+1).$$ We obtain $$n = 2^4 \cdot 3^4 \cdot 5^2 \cdot 7^2 \cdot 11^2 \cdot 13^2 = 32464832400.$$ We claim that this is the number $n_0$.

We prove this by considering a case separation based on the value of $\alpha_1$ in the prime decomposition of $n_0$. Note that since $$\log_2 32464832400 \approx 34.9,$$ we must have $\alpha_1 ≤ 34$. As $\alpha_1 +1$ divides $2025$, it must be one of $27, 25, 15, 9, 5, 3$.

Assume $\alpha_1 + 1 = 27$. Since we have $\frac{2025}{27}=75 = 5^2 \cdot 3$, $\alpha_2+1$ is at least $5$. Note that if $\alpha_2+1$ is at least $15$, we have $n >= 2^{26} \cdot 3^{14} > 2^{35} > 32464832400.$ If on the other hand $\alpha_2+1 = 5$, we have the only possible decomposition $2025 = 27 \cdot 5 \cdot 5 \cdot 3$ and $n = 2^{26} \cdot 3^4 \cdot 5^4 \cdot 7^2 > 2^{35} > 32464832400.$ Thus, this cannot give us $n_0$.

Assume $\alpha_1 + 1 = 25.$ Since we have $\frac{2025}{25}=81 = 3^4$, $\alpha_2+1$ is at most $9$. Note that if $\alpha_2 +1 $ is $9$, we have that $\alpha_3$ is at least $3$ and $n >= 2^{24} \cdot 3^8 \cdot 5^2 > 2^{35} > 32464832400$. If $\alpha_2 +1 = 3$, the only possible decomposition is $2025 = 25 \cdot 3 \cdot 3 \cdot 3 \cdot 3$ and $n=2^{24} \cdot 3^2 \cdot 5^2 \cdot 7^2 \cdot 11^2 > 2^{35} > 32464832400.$ Thus, this also cannot give us $n_0$.

Assume $\alpha_1 + 1 = 15.$ Since we have $\frac{2025}{15}=135 = 5 \cdot 3^3$, $\alpha_2+1$ is at most $15$. Note that if $\alpha_2 +1 $ is $15$, we have $n >= 2^{14} \cdot 3^{14} \cdot 5 > 2^{35} > 32464832400.$ If $\alpha_2 +1 =9$, then the only possible decomposition is $2025 = 15 \cdot 9 \cdot 5 \cdot 3$ and $n = 2^{14} \cdot 3^{8} \cdot 5^4 \cdot 7^2 = 3292047360000 > 2^{35} > 32464832400.$ If $\alpha_2 + 1 = 5$, then the only possible decomposition is $2025 = 15 \cdot 5 \cdot 3 \cdot 3 \cdot 3$ and $n = 2^{14} \cdot 3^4 \cdot 5^2 \cdot 7^2 \cdot 11^2 = 196709990400 > 2^{35}.$ Thus, this also cannot give us $n_0$.

Assume $\alpha_1+1 = 9$. Since we have $\frac{2025}{9}=225 = 5^2 \cdot 3^2$, $\alpha_2+1$ is at most $9$ and at least $5$. If $\alpha_2 +1 =9$, then the only possible decomposition is $2025 = 9 \cdot 9 \cdot 5 \cdot 5$ and $n = 2^{8} \cdot 3^{8} \cdot 5^4 \cdot 7^4 = 2520473760000 > 2^{35}> 32464832400.$ If $\alpha_2 +1 =5$, then the only possible decomposition is $2025 = 9 \cdot 5 \cdot 5 \cdot 3 \cdot 3$ and $n = 2^8 \cdot 3^4 \cdot 5^4 \cdot 7^2 \cdot 11^2 = 76839840000 > 32464832400.$ Thus, this cannot give us $n_0$ either.

The only possible decomposition with $\alpha_1 + 1 <= 5$ is the one we which gives $n=32464832400$, which must therefore be the minimal number $n_0$ with $2025$ divisors.

As it is below $2^{2025}$, this is our final answer.

Answer: 32464832400.

Mathsbombe Competition 2025 is organised by the The Department of Mathematics at The University of Manchester.
© The University of Manchester 2012–2025, All Rights Reserved
Contact us | Privacy notice