Analysis, geometry and dynamical systems
Our research describes properties of geometric structures and develops the theory and applications of dynamical systems.
PhD projects
We welcome applications for PhD study in all areas of analysis, geometry and dynamical systems.
Before applying, visit the 'areas of expertise' pages listed below to find out more about potential PhD supervisors.
PhD enquiries related to this theme can be directed to Dr Joel Daou (applied and numerical analysis projects) and Dr Marcus Tressl (pure mathematics projects).
We work with international colleagues to understand problems in geometry, ergodic theory and dynamical systems.
These ideas are applied in other areas such as number theory, quantum field theory, classical mechanics and the biological sciences.
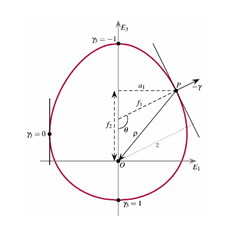
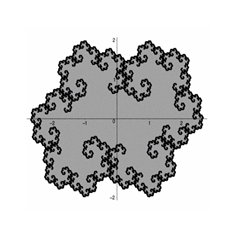
Our research interests include the study of fractals and fractal dimensions, symplectic structures, supermanifolds, symmetry and differential equations.
Areas of expertise
-
Analysis and geometry
Analysis and geometry are core areas of mathematics which are also key to understanding many areas of theoretical physics.
Read more
-
Dynamical systems
Dynamical systems describes time dependent behaviour, including chaos, in difference and differential equations and has applications across the sciences.
Read more
-
Ergodic theory and dimension
Ergodic theory gives a probabilistic view of dynamics via measures. Different definitions of dimensions are used to characterize complicated (fractal) structures.
Read more
Research outputs
Find the Department's recent publications in the University's database.
Search
Postgraduate research
Discover the PhD opportunities available in the Department of Mathematics.
Read more
Research seminars
Research seminars on topics associated with analysis, geometry and dynamical systems take place regularly in the following series: